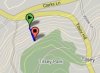
I've got to bottom of what is causing the Sanoodi gradient error over short distances, and it's what I call the "tail" effect. Here's the explanation. Have a look at the first image below and then refer to the text below that. The contour lines colour has been changed to black as the standard Sanoodi colour would not reproduce online from a copied image, probably deliberate:
You can see I've again put a row of evenly spaced markers on quite evenly spaced contour lines on a steep and even 1 in 3.6 slope. The gradient graph alongside shows a different picture, the slope between each pair of markers being shown as anything from fractionally uphill to a sheer downhill drop, clearly very wrong.
The reason is quite simple. The line between each pair of markers crosses only one contour line so Sanoodi cannot judge the gradient from that. The loose "tail" at the side of the line reports randomly therefore and can give almost any result. Since the next section has to start at the correct point relating to the overall slope, the error on the first part of the line has to be compensated on the second part, so that second part is forced into an inaccurate slope to compensate. After that the slopes between markers are roughly correct until the final "tail" which can go haywire as the graph above shows.
Sanoodi's algorithm cannot ignore sections which cross only one contour line, since if it did that it would often be unable to report in fairly flat territory. However, Sanoodi's creators have put in one error correction to minimise the problem. When a section is overall downhill, any individual error is not allowed to report completely the opposite way, any opposite trend being held to about 5% maximum, and you can see that at the point in the elevation graph above where a line section tries to go uphill but is restricted.
Over distance there's no problem. Any error across a contour line is restricted to the 10 metre elevation between two contour lines. Therefore it's a serious error if the distance across the ground is short, such as 20 metres, since it could report that as roughly flat or a 50% sheer slope. If one contour is crossed, again with the same possible error, but the line is 400 meters across the ground, the error can be reported as roughly flat again or only a 2.5% slope, a tiny variation which is scarcely noticeable.
Now have a look at the next image below and refer to it's text:
Here I've thinned out the markers, and you'll see that between each pair the line crosses two 10 metre contour sections. Therefore there's one loose "tail" to each graph line section giving an error from flat to 10 metres change averaged against two correct 10 metre sections. This gives the graph shown, in which the errors of the two slope lines are greatly reduced.
Finally now the third image below and it's text:
Here there's only two markers giving one line on the graph, so we now have two "tail" errors on the line. However, the line crosses five ten metre elevation sections, so the maximum imposed error can only be 1 part in 5 and on average will be half that, a barely noticeable deviation. As can be seen and calculated, the slope is being reported on the graph as roughly correct, as it was overall on all three graphs.
So in conclusion, a line between any two markers on Sanoodi needs length (distance), or if short, it needs to cross as many contour lines as possible between any pair of markers if results are to be accurate.
.